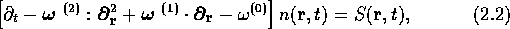
where the various terms have been introduced in section
. The state of the art of swarm theory, as
far as analysis of experiments is concerned is expounded in
Huxley and Crompton [1974].
This is based on the diffusion equation
where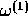 
is the total reaction rate,
the drift velocity, and
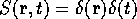the diffusion tensor. This
equation is exactly solvable, whose solution for an initial
delta function pulse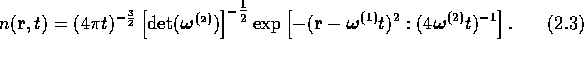 
is a displaced Gaussian
The hydrodynamic assumption () leads to the
transport equation
which is a generalization of the diffusion equation. This
follows from () if we identify the transport
coefficients
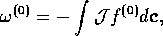with
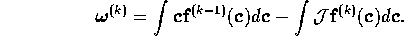
That hydrodynamic transport should be governed by the infinite
multipole transport equation () and that the
diffusion equation was but an approximation truncated
at second order, was pointed out by Kumar and Robson
[1973]. Skullerud [1974] developed the
transport
equation into a theory that explained anisotropies observed
earlier in Monte Carlo experiments
[MacIntosh
[1974]]
.
The first steps beyond the hydrodynamic assumption () were taken by such people as MacIntosh [1974] who
studied the effect of initial value conditions by Monte Carlo
techniques, and Skullerud [1974,1977] who used
numerical
solutions to the Boltzmann equation. A significant improvement
in technique came with the introduction of time dependent
transport coefficients
[Tagashira et al.
[1977],
Tagashira
[1981]]
. These workers have suggested that
different transport coefficients are applicable to the different
type of swarm experiments. This debate has largely been settled
by expressing the various transport coefficients in terms of the time of
flight parameters [Blevin and Fletcher
[1984]] .
The next major step in the development of a non-hydrodynamic
theory comes with Kumar [1981], who relates the
characteristic time of the approach to the hydrodynamic regime
to the inverse of a gap in the spectrum of 
between the lowest
eigenvalue, and the rest
of the spectrum. Kondo [1987]
introduced a projection operator which projected out the hydrodynamic
solution.
This work is a restatement of adiabatic elimination methods
[Marchesoni and Grigolini
[1985]]
in a swarm context.
Kondo's paper is general, and the formal nature of the work does not
properly address the conditions under which the hydrodynamic
regime might exist, or what the timescales of the approach to
the hydrodynamic regime might be. We can answer some of these
questions by making the simplifying assumption that the spectrum
of 
is discrete, and that the set of eigenfunctions is
complete in the space of all velocity distributions, and that
one eigenvalue has smaller real part than all the others. This
work has been published as Standish [1987].
