The Chapman-Enskog procedure alluded to earlier provides a way of passing from the mesoscopic picture of the Boltzmann equation to the hydrodynamic picture. In the theory of neutral gases, there are two timescales, the first being the mean free time between collisions, and the second a macroscopic time which depends on the size of the system under consideration. This macroscopic time might be, for example, the time taken for a gas to equalize its pressure after being let into an empty box. The approach to equilibrium occurs in two stages. The first stage is the approach to a local thermal equilibrium on a timescale of the order of the mean free time. The distribution function approaches that of a local Maxwellian,
where n is the local gas number density, T the local
temperature,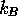 
the local velocity field,
Boltzmann's constant and m the molecular mass. The
second stage, occurring on a macroscopic timescale, is
described by the relaxation of the functions n, T, and
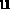to their uniform equilibrium values.
The Chapman-Enskog solution of the Boltzmann equation uses the smallness of the mean free time as a perturbation parameter. On successive iterations of this perturbation, one obtains the Euler, Navier-Stokes, Burnett and Super-Burnett hydrodynamics respectively. See Chapman and Cowling [1970].
In swarm physics, the linear Boltzmann equation has an analogous solution. There are two timescales, a mean free time, and a macroscopic time which is usually the drift time. Since energy is constantly being extracted from the electric field, there is no approach to equilibrium. However, after several collision times, the velocity distribution will relax to a ``local steady state'', in which the energy being extracted from the field by the swarm is removed by collisions with the background gas. This state is called the hydrodynamic regime by analogy with the hydrodynamics of neutral gas theory.
Instead of the five fields (n, T, and the three components
of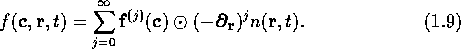 
) of the neutral gas theory, the
space-time dependence of a swarm in the hydrodynamic regime is
carried by the density alone:
Here the 
are rank j tensor functions
of 
.
It should be noted that equation (
) is the
complete description of the hydrodynamic regime. By contrast,
the hydrodynamic regime of the neutral gas problem is described
by a coupled set of equations in the five fields (n, T and
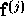). The Chapman-Enskog method constructs
these equations at successive levels of approximation (Euler,
Navier-Stokes etc.). Similarly, a coupled set of equations can
be derived for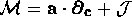 
with the operator 
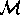playing a rôle similar to the rôle that the linearized
collision operator plays in neutral gas theory.
