




Next: End Effects in
Up: The Linear Boltzmann
Previous: The nature of
As a way of obtaining insight into how the behaviour of swarms are related
to
various mathematical features of the Boltzmann equation, it is useful to
have
an exactly solvable model. The models most often employed in transport
theory
are briefly reviewed in section 13 of Kumar et al.
[1980]. The model that reflects best the theory
developed so far is the Rayleigh gas model, which describes Brownian
motion.
Brownian motion may be considered to be a limiting case of swarms in which
the
diffusing particle is very much more massive than the background fluid
molecules. This phenomenon is described in stochastic theory by the
master
equation, which is an integral equation, and an equivalence with
a differential
form, known as the Kramers-Moyal expansion. This expansion is often
truncated
at second order, where it is known as the Fokker-Planck equation, which is
essentially exact for Brownian motion. A general introduction to this
subject
can be found by Risken [1984], and in a kinetic theory context by
Braglia [1980].
The analogy of Brownian motion and swarm physics suggests that a
differential
form of the collision operator can be found in which the ratio  plays
the part of a small expansion parameter, where M is the background gas
molecule
mass, and m the charged particle mass. Kumar et al.
[1980] develop this
expansion, which they call the Fokker-Planck expansion, and another
expansion
valid when
plays
the part of a small expansion parameter, where M is the background gas
molecule
mass, and m the charged particle mass. Kumar et al.
[1980] develop this
expansion, which they call the Fokker-Planck expansion, and another
expansion
valid when  is small.
is small.
If we make the approximation of the background gas molecule velocities
being
much larger that the charged particle velocities, and truncate the
Fokker-Planck expansion at second order, we obtain the Klein-Kramers
equation:

The reaction rate 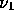 is positive
when ionization occurs. The coefficients
is positive
when ionization occurs. The coefficients  and
and 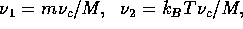 are related
to
physical quantities by
are related
to
physical quantities by

where  is Boltzmann's constant and T the background gas
temperature.
The
collision frequency
is Boltzmann's constant and T the background gas
temperature.
The
collision frequency 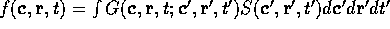 is approximately the product of the swarm drift velocity,
the background gas number density, and the collision cross section.
is approximately the product of the swarm drift velocity,
the background gas number density, and the collision cross section.
We look for a solution to the Klein-Kramers equation in the form

where the Greens function G satisfies
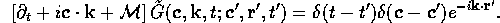
Taking the Fourier transform of ( ) with respect to
position, we find:
) with respect to
position, we find:

The operator 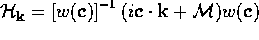 can be
transformed into a hermitian operator by means of the similarity
transformation
can be
transformed into a hermitian operator by means of the similarity
transformation 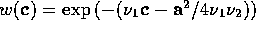 , where
, where 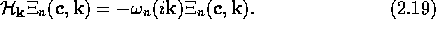 .
This has a discrete spectrum with a complete set of eigenfunctions:
.
This has a discrete spectrum with a complete set of eigenfunctions:
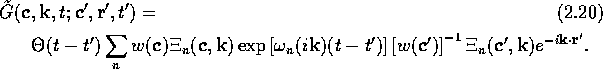
The Green's function can then be written using a spectral expansion

Making the change of variables

the eigenvalue equation ( ) for
) for 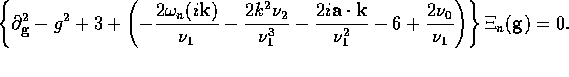 is transformed to the harmonic oscillator problem
familiar from quantum mechanics:
is transformed to the harmonic oscillator problem
familiar from quantum mechanics:

This equation is separable in cartesian coordinates  ,
,
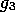 ,
,  and has solutions in terms of Hermite polynomials
[Abramowitz and Stegun
[1965] 22.6.20]
:
and has solutions in terms of Hermite polynomials
[Abramowitz and Stegun
[1965] 22.6.20]
:


where 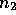 ,
,  and
and 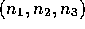 are whole numbers, and n is the
cartesian triple
are whole numbers, and n is the
cartesian triple  . These solutions can also be
expressed in spherical coordinates by means of Burnett functions
[Kumar
[1980]]
. In one dimension, the result is
identical
except that g is now a scalar, and the index set
. These solutions can also be
expressed in spherical coordinates by means of Burnett functions
[Kumar
[1980]]
. In one dimension, the result is
identical
except that g is now a scalar, and the index set 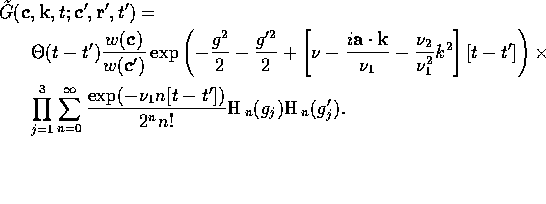 is
the set of whole numbers.
is
the set of whole numbers.
The Greens function may now be evaluated by substituting
( ) and (
) and ( ) into (
) into ( ):
):
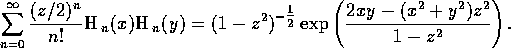
The sum over n may be evaluated using a generating function
for Hermite polynomials [Erdélyi
[1954]
10.13.22]
:
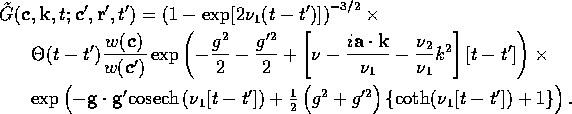
Thus we obtain

The inverse Fourier transform of 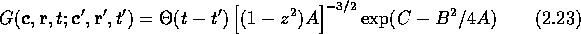 is a Gaussian
integral, so we obtain
is a Gaussian
integral, so we obtain

where  and
and
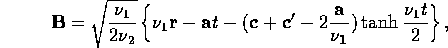
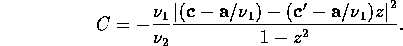

In one dimension, the exponent on the second factor in
( ) is
) is 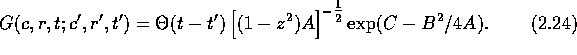 , i.e.
, i.e.

Figure ( ) shows the one dimensional density distribution
plotted at successive values of t, from an initial delta
function pulse, i.e.
) shows the one dimensional density distribution
plotted at successive values of t, from an initial delta
function pulse, i.e.

In the r-t plane, the path that the centroid traces out is plotted
(dotted
curve) and can be compared with the path expected if the system were
hydrodynamic with a constant drift velocity (dashed curve).
Non-hydrodynamic effects manifest themselves within time  of the origin, with a residual constant retardation of the
swarm at large times. This was an effect first observed by Harris
[1981],
who noted the ``non-diffusive'' nature of the Klein-Kramers equation at
large
times. Titulaer [1983] explained the phenomenon using a
detailed
analysis of the Klein-Kramers equation. This effect has been discovered a
number of times in different contexts, for example Robson [1975]
noted
the effect in the BGK model. However, it was generally ignored as not
having
physical consequences. I rediscovered this phenomenon
independently, and showed that it should occur under quite general
circumstances and have measurable consequences for swarm experiments.
More will be said on this in chapter
of the origin, with a residual constant retardation of the
swarm at large times. This was an effect first observed by Harris
[1981],
who noted the ``non-diffusive'' nature of the Klein-Kramers equation at
large
times. Titulaer [1983] explained the phenomenon using a
detailed
analysis of the Klein-Kramers equation. This effect has been discovered a
number of times in different contexts, for example Robson [1975]
noted
the effect in the BGK model. However, it was generally ignored as not
having
physical consequences. I rediscovered this phenomenon
independently, and showed that it should occur under quite general
circumstances and have measurable consequences for swarm experiments.
More will be said on this in chapter  .
.
Figure: Evolution of the one dimensional Klein-Kramers equation showing
non-hydrodynamic effects at large times





Next: End Effects in
Up: The Linear Boltzmann
Previous: The nature of
Russell Standish
Thu May 18 11:43:52 EST 1995
 plays
the part of a small expansion parameter, where M is the background gas
molecule
mass, and m the charged particle mass. Kumar et al.
[1980] develop this
expansion, which they call the Fokker-Planck expansion, and another
expansion
valid when
plays
the part of a small expansion parameter, where M is the background gas
molecule
mass, and m the charged particle mass. Kumar et al.
[1980] develop this
expansion, which they call the Fokker-Planck expansion, and another
expansion
valid when  is small.
is small.

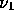 is positive
when ionization occurs. The coefficients
is positive
when ionization occurs. The coefficients  and
and 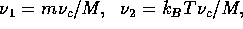 are related
to
physical quantities by
are related
to
physical quantities by

 is Boltzmann's constant and T the background gas
temperature.
The
is Boltzmann's constant and T the background gas
temperature.
The 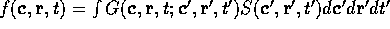 is approximately the product of the swarm drift velocity,
the background gas number density, and the collision cross section.
is approximately the product of the swarm drift velocity,
the background gas number density, and the collision cross section.

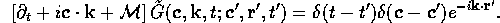

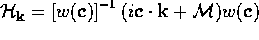 can be
transformed into a hermitian operator by means of the similarity
transformation
can be
transformed into a hermitian operator by means of the similarity
transformation 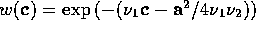 , where
, where 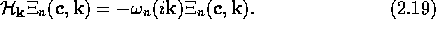 .
.
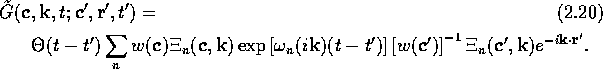


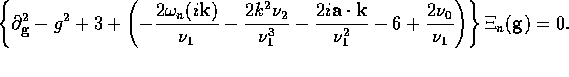 is transformed to the harmonic oscillator problem
is transformed to the harmonic oscillator problem

 ,
,
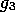 ,
,  and has solutions in terms of Hermite polynomials
and has solutions in terms of Hermite polynomials


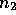 ,
,  and
and 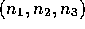 are whole numbers, and n is the
cartesian triple
are whole numbers, and n is the
cartesian triple  . These solutions can also be
expressed in spherical coordinates by means of Burnett functions
. These solutions can also be
expressed in spherical coordinates by means of Burnett functions
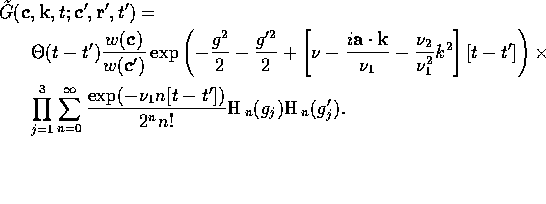 is
the set of whole numbers.
is
the set of whole numbers.
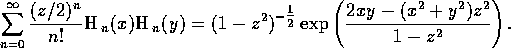
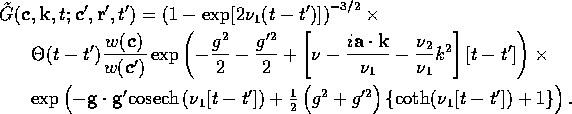

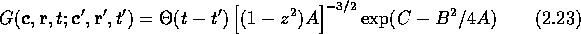 is a Gaussian
integral, so we obtain
is a Gaussian
integral, so we obtain

 and
and
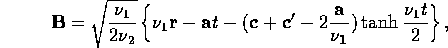
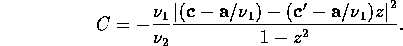

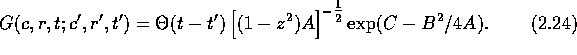 , i.e.
, i.e.


 of the origin, with a residual constant retardation of the
swarm at large times. This was an effect first observed by Harris
[
of the origin, with a residual constant retardation of the
swarm at large times. This was an effect first observed by Harris
[