Here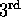 
is a rank six tensor that is clearly
symmetric with respect to interchanges of the 
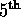and
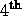, and of the 
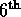and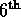 
indices.
An arbitrary isotropic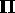 
rank tensor has 15
independent components [Eu
[1979]]
,
which is reduced
to 7 components when the above symmetries are taken into account
(see Appendix 
).If we further suppose that the fluid
is monatomic, then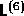 
must be symmetric, and the
number of independent components reduces to 5, of which two are
diagonal in the first two indices, and three are traceless. So at
second order in the strain rate, there are five transport
coefficients, two of which refer to bulk properties, and the
other three which describe shearing properties. Similarly, at the
next order in strain rate, there will be 22 transport
coefficients.
Burnett [1935] developed a form of hydrodynamics that was more accurate than Navier-Stokes hydrodynamics by applying the Chapman-Enskog procedure to the Boltzmann equation. [See Chapter 7 and 15 of Chapman and Cowling
[1970]
for a
discussion]
. This introduced 19 transport coefficients of which
the 8 bulk coefficients are zero for a dilute gas. This left 6
coefficients for the correction to the viscous pressure tensor,
and 5 for the thermal flux term. The constitutive relation
() refers to a situation where there are
no thermal or pressure gradients, and so the three shear
components of 
can be identified with the
remaining three Burnett coefficients in equation (15.3,8) of
Chapman and Cowling [1970]. More will be
said of the non-linear Burnett coefficients in chapter
, where tractable expressions are developed
relating the coefficients to equilibrium correlation functions.
The generalization of the constitutive relation () for swarms is different in that linearity in the swarm density
must
be preserved:
Here the generalized transport coefficients
are rank l tensors, and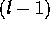 
indicates the 
-fold scalar
product.
A fully consistent derivation of this relation based on a
Chapman-Enskog-like solution of the linear Boltzmann equation can
be found in Kumar et al. [1980].
It is thought that the higher order
transport coefficients 
, with
, play a role only where the density gradients are
not small, such as near the boundary of the apparatus containing the
swarm. However, at large density gradients, this whole approach is
doubtful, as non physical behaviour results [see
[1974]]
. Analogous problems occur with Burnett and
Super-Burnett level hydrodynamics in the theory of neutral
gases [see
[1983]]
.
More will be discussed on the subject of higher-order transport
coefficients in chapter
,
where certain experimental effects can be explained in
terms of these coefficients.
