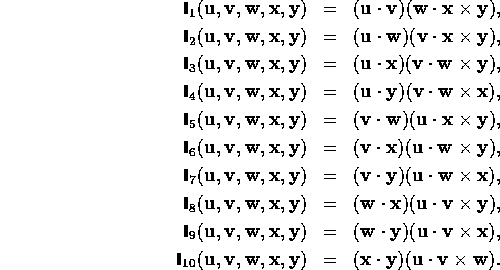
), and odd tensors as a linear combination of products of the
unit tensor and the Levi-Cevita, or determinant tensor (
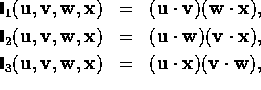). This result is based on Weyl's theory of invariant
polynomials [see Temple
[1960] for a discussion]
. In
practice, this means finding every possible way of writing products of
inner products between pairs of vectors, so that for example, the space of
isotropic rank four tensors will be spanned by:
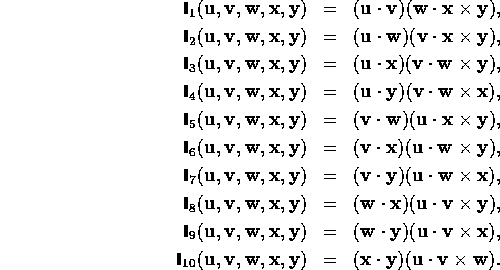
and that the space of rank five isotropic tensors is spanned by:
Because the generalized constitutive relation (
) must be
symmetric with respect to changes in sign of the thermodynamic force and
flux, we are only interested in even rank tensors. I have written a
program that generates the isotropic tensors of arbitrary even rank, and
then proceeds to apply symmetrization operations to the tensors to produce
the final set of independent tensors. Modifying it to produce odd rank
tensors should not be too difficult a task.
An example of its use, may be found
in finding the number of transport coefficients used to describe the
second order Burnett coefficient between stress and strain. This
coefficient connects a second rank stress tensor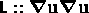 
with the
square of a second rank strain tensor. The coefficient is thus of sixth
rank. There are fifteen sixth rank isotropic tensors, but not all of them
are valid candidates because the only non-vanishing components must be
symmetric with respect to interchanges of the third and fifth argument, as
well as the fourth and the sixth. This is the case because in the
expression 
, interchanging the two
s produces no effect, neither the two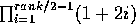 
s. In the program,
this is performed by the lines
In the case of a monatomic fluid, we may further expect that the tensor should be symmetric with respect to the first two indices.Symmetrize(LinComb[i], 3, 5); Symmetrize(LinComb[i], 4, 6);
The program listing following can be used for arbitrary rank by changing
the constants rank, NoComp and NoCompp1. Rank is fairly obviously the
tensorial rank of the tensor under study. NoComp is the number of
independent isotropic tensors of that rank, given by
.
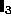In the program, the basis tensors are represented as an array with rank
components of type integer, which contain the sequence of vectors involved
in the inner products. For example,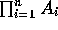 
in the rank four case
would be represented by the integer sequence 1423. The complete basis is
generated in the calcTensors procedure, and stored in Tensors. It does
this by generating all possible permutations of the rank vectors, then
expressing them all in a canonical form in which each pair is ordered so
that the lowest index comes first within the pairs, and the pairs are then
ordered according to the first index in each pair. When the canonical form
is found, it is checked against a list of all previous canonical tensors
found, and only added to the list if it is found to be distinct.
To generate the symmetrized tensors, we store the coefficients of a linear combination of the basis tensors in variables of type LinType. The algorithm proceeds by taking every basis tensor corresponding to non-zero coefficients, swapping the indices to be symmetrized, placing the tensor in canonical form, comparing this result against the basis list to find which tensor it corresponds to, then adding the original non-zero coefficient to the slot corresponding to the swapped basis tensor.
program tensors;
{even rank version}
const
rank = 6;
NoComp = 15; {NoComp = (rank-1)(rank-3)...3}
NoCompp1 = 16; {NoComp+1}
type
jvalType = set of 2..rank;
TensorType = array[1..rank] of integer;
LinType = array[1..NoComp] of integer;
var
tensor: array[1..NoCompp1] of TensorType;
i, j: integer;
TensorIndex: integer;
zero: LinType;
LinComb: array[1..NoComp] of LinType;
out: text;
procedure swap (var x, y: integer);
var
t: integer;
begin
t := x;
x := y;
y := t;
end;
procedure Sort (left, right: integer; var Tensor: TensorType);
{Yep, the good old Qsort routine copied from ATPUG issue 1}
var
II, JJ, temp: integer;
Pivot: integer;
IIisGTright, JJisLTleft, IIgreatThan: boolean;
begin
II := left;
JJ := right;
pivot := Tensor[pred(2 * ((II + JJ) div 2))];
repeat
while Tensor[pred(2 * II)] < pivot do
II := succ(II);
while Tensor[pred(2 * JJ)] > pivot do
JJ := pred(JJ);
if II <= JJ then
begin
swap(Tensor[2 * II - 1], Tensor[2 * JJ - 1]);
swap(Tensor[2 * II], Tensor[2 * JJ]);
II := succ(II);
JJ := pred(JJ);
end;
until II > JJ;
if JJ > left then
Sort(left, JJ, Tensor);
if II < right then
Sort(II, right, Tensor)
end;
function eq (x, y: tensorType): boolean;
var
i: integer;
result: boolean;
begin
result := true;
for i := 1 to rank do
result := result and (x[i] = y[i]);
eq := result;
end;
function eqL (x, y: LinType): boolean;
var
i: integer;
result: boolean;
begin
result := true;
for i := 1 to NoComp do
result := result and (x[i] = y[i]);
eqL := result;
end;
procedure canonical (var tensor: tensortype);
var
j: integer;
begin
{order each pair}
for j := 1 to rank div 2 do
if tensor[2 * j - 1] > tensor[2 * j] then
swap(Tensor[2 * j - 1], Tensor[2 * j]);
sort(1, rank div 2, Tensor);
end;
procedure calcTensors;
var
TTensor: TensorType;
{TensorIndex: integer;}
procedure GenerLoop (nest: integer; jvals: jvaltype; TTensor: tensorType);
var
j, k: integer;
begin
for j := (nest + 2) div 2 to rank do
if not (j in jvals) then
begin
TTensor[nest] := j;
if nest < rank then
GenerLoop(succ(nest), jvals + [j], TTensor)
else
begin
canonical(TTensor);
k := 1;
while not eq(TTensor, Tensor[k]) and (k < TensorIndex) do
k := succ(k);
if k = TensorIndex then
begin
if TensorIndex > NoComp then
writeln('Either I stuffed up,',
' or you guessed the wrong value for NoComp');
tensor[k] := TTensor;
TensorIndex := succ(TensorIndex);
end;
end; {of else}
end; {of if not (j in jval)}
end; {of GenerLoop}
begin
TensorIndex := 1;
TTensor[1] := 1;
GenerLoop(2, [], TTensor);
end;
procedure symmetrizePairs (var LinComb: LinType; pr1, pr2: integer);
{Symmetrize tensor with respect to two pairs of indices}
var
NewLin: LinType;
i, j: integer;
TTensor: TensorType;
begin
NewLin := zero;
for i := 1 to NoComp do
if LinComb[i] > 0 then
begin
{get representation of component}
TTensor := Tensor[i];
{swap pairs 1 and 2}
for j := 1 to rank do
if TTensor[j] = 2 * pr1 then
TTensor[j] := 2 * pr2
else if TTensor[j] = pred(2 * pr1) then
TTensor[j] := pred(2 * pr2)
else if TTensor[j] = 2 * pr2 then
TTensor[j] := 2 * pr1
else if TTensor[j] = pred(2 * pr2) then
TTensor[j] := pred(2 * pr1);
canonical(TTensor);
{find TTensor in the list}
j := 0;
repeat
j := j + 1
until eq(TTensor, Tensor[j]);
{add the swapped part to make it symmetric}
NewLin[j] := NewLin[j] + LinComb[i];
end; {of for i:=1 to NoComp}
{add NewLin to LinComb}
for i := 1 to NoComp do
LinComb[i] := LinComb[i] + NewLin[i];
end; {of symmetrizePairs}
procedure symmetrize (var LinComb: LinType; Index1, Index2: integer);
{Symmetrize tensor with respect to two indices}
var
NewLin: LinType;
i, j: integer;
TTensor: TensorType;
begin
NewLin := zero;
for i := 1 to NoComp do
if LinComb[i] > 0 then
begin
{get representation of component}
TTensor := Tensor[i];
{swap pairs 1 and 2}
for j := 1 to rank do
if TTensor[j] = Index1 then
TTensor[j] := Index2
else if TTensor[j] = Index2 then
TTensor[j] := Index1;
canonical(TTensor);
{find TTensor in the list}
j := 0;
repeat
j := j + 1
until eq(TTensor, Tensor[j]);
{add the swapped part to make it symmetric}
NewLin[j] := NewLin[j] + LinComb[i];
end; {of for i:=1 to NoComp}
{add NewLin to LinComb}
for i := 1 to NoComp do
LinComb[i] := LinComb[i] + NewLin[i];
end; {of symmetrize}
begin
CalcTensors;
for i := 1 to NoComp do
zero[i] := 0;
for i := 1 to NoComp do
begin
LinComb[i] := zero;
LinComb[i][i] := 1;
Symmetrize(LinComb[i], 1, 2);
Symmetrize(LinComb[i], 3, 5);
Symmetrize(LinComb[i], 4, 6);
j := 0;
repeat
j := succ(j)
until eqL(LinComb[j], LinComb[i]);
if i = j then {the linear combination is unique, so output it}
begin
for j := 1 to NoComp do
if LinComb[i][j] <> 0 then
write(LinComb[i][j] : 1, '*I(', j : 3, ')+');
writeln;
end;
end;
end.