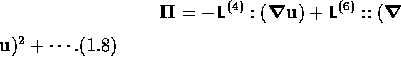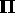The non-equilibrium part of the pres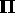sure tensor 
is
called the viscous pressure tensor
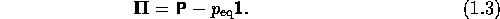
Two centuries ago Newton realised that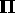 
, which is zero
at equilibrium, can be driven by the strain rate tensor 
. For atomic fluids close to equilibrium, the most
general linear relation between the viscous pressure tensor and
the strain rate tensor is
The fourth rank transport tensor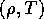 
is a function of the
thermodynamic state of the system 
. It is independent
of the strain rate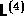 
. In fluids with no external field
applied,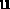 
must be
isotropic, i.e. rotationally invariant.
There are three independent isotropic rank four tensors, [see
Temple
[1960]]
defined by the possible multilinear
invariants of four vectors 
, 
, 
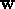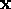and
:
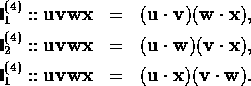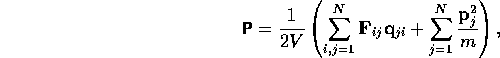
In atomic fluids, the force acting between atoms is parallel to the displacement between the atoms, i.e. a central force. This implies that P
is symmetric
,
and so (
) becomes
where 
is the shear viscosity and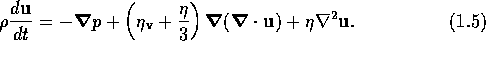 
is the
bulk viscosity. In molecular fluids, the intermolecular forces do
not necessarily act parallel to the displacement between the
molecules and the pressure is not necessarily symmetric, so a
further term, vortex viscosity [de Groot and Mazur
[1962]] must be introduced.
The continuity relation () gives an
exact relationship between the velocity field and the pressure
tensor. The Newtonian constitutive relation gives a relation
between the pressure tensor and the velocity field which is a good
approximation
for fluids close to equilibrium. By combining the continuity and
Newtonian constitutive relations, we obtain the Navier-Stokes
equation of hydrodynamics:
In swarm physics, the only conserved quantity is mass (or
equivalently charge), and even then only in the absence of reactions.
The mass continuity equation is
() with an additional term of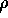 
on the right hand
side representing the net production of swarm particles due to reactions
with the background gas. A momentum continuity equation would need to
take into account the dynamics of the background gas, and so is not a
useful relation for the theory. In this case, the constitutive relation
must
contain a constant term representing the average streaming
velocity due to the electric field, as well as the term
proportional to the gradient of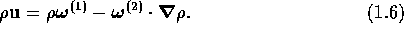 
:
Upon substituting () into (), we
obtain the diffusion equation:
The transport coefficients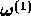 
,
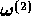and
can be identified with the reaction
rate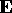 
, the
system drift velocity and the coefficient of diffusion respectively. In free
space, the transport coefficients of the swarm must satisfy
cylindrical symmetry with the major axis in the direction of the
electric field. The only vectors with this property must be
proportional to the electric field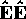 
, and that any second
rank tensor must be a linear combination of the unit tensor, and
of the dyad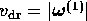 
. This means that the transport
coefficients can be represented by three parameters: the drift
velocity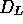 
and the two
components of the diffusion coefficient, namely that which is aligned
with the field,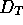 
, and that which is transverse to the field
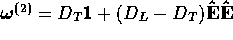. We have 
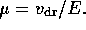. An alternative parameter to the drift
velocity is
the mobility: 
