
The equations of motion used to generate the flux-statted dynamics in general will be of the form
The intermolecular forces are given by 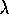 . In these
equations,
. In these
equations,  and
and 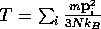 are computed by a Nosé-Hoover feedback
mechanism to keep the flux J, and the temperature
are computed by a Nosé-Hoover feedback
mechanism to keep the flux J, and the temperature
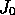
fluctuating about fixed mean values 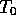 and
and  . Specifically, we have
. Specifically, we have
 and
and
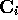 The phase variables
The phase variables 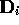 and
and 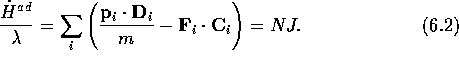 are are chosen so that
are are chosen so that

For example, in the case of constant colour current dynamics,  , where
, where 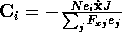 is the charge on the ion, and
is the charge on the ion, and
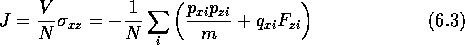
. In the case of stress-statted dynamics [Brown and Clarke [1986] , Hood et al. [1987]] , the flux to be kept constant is the xz component of the stress tensor, namely
with 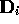 and
and 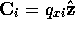 given by
given by 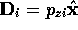 and
and 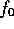 .
.
Consider an initial ensemble characterized by the distribution function
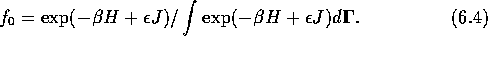 ,
,

If we assume adiabatic incompressibility of phase space
(AI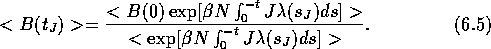 ), then the Kawasaki expression for the average of an
arbitrary phase variable, B, can be derived
[Morriss and Evans
[1985]]
), then the Kawasaki expression for the average of an
arbitrary phase variable, B, can be derived
[Morriss and Evans
[1985]]
Here the subscript J denotes that 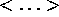 is evolved
under constant flux dynamics. The ensemble average
is evolved
under constant flux dynamics. The ensemble average  is taken with respect to the distribution function
is taken with respect to the distribution function 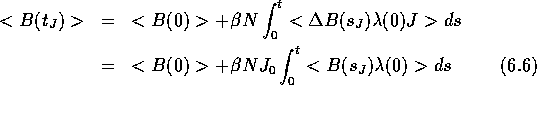 .
.
By differentiating and reintegrating (![]() ) in the usual
way, a transient time correlation function expression for the
nonequilibrium phase average is generated. Thus
) in the usual
way, a transient time correlation function expression for the
nonequilibrium phase average is generated. Thus
in the thermodynamic limit, where 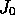 . Since the
flux-statted propagators do not depend on the average flux
. Since the
flux-statted propagators do not depend on the average flux 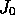 , the
only dependence on
, the
only dependence on 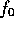 in the above expression is either
explicit, or comes in indirectly through
in the above expression is either
explicit, or comes in indirectly through 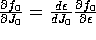 . By the chain rule,
. By the chain rule,
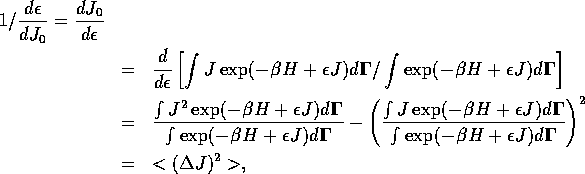
. The first derivative can be evaluated by the inverse function theorem

and the second derivative is simply

So

The derivatives of (![]() ) with respect to
) with respect to 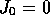 can be
easily evaluated around
can be
easily evaluated around 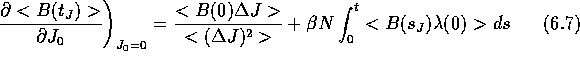 , and the first three are:
, and the first three are:
In comparing these results with Evans and Lynden-Bell
[1988], it should be noted that one is interested in
computing
the phase average of the force required to maintain a steady
current. This phase variable is antisymmetric with respect to a
reflection in space, whereas J is independent of position, and
so all the averages of the form 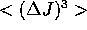 will vanish.
Similarly,
will vanish.
Similarly,  and all odd moments of J will
vanish. The quantity
and all odd moments of J will
vanish. The quantity 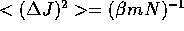 can be evaluated, and is
found to be
can be evaluated, and is
found to be 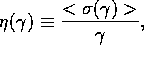 .
.
Similar simplifications will also apply with the case of planar Couette flow, where one is attempting to deduce the nonlinear viscosity, defined by

where 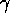 is the shear stress, and
is the shear stress, and 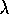 the
strain rate associated with it.
Both
the
strain rate associated with it.
Both  and J are antisymmetric under a reflection in
the x direction in both position and velocity space
and J are antisymmetric under a reflection in
the x direction in both position and velocity space
 ), but
under a time reversal
), but
under a time reversal  ,
, 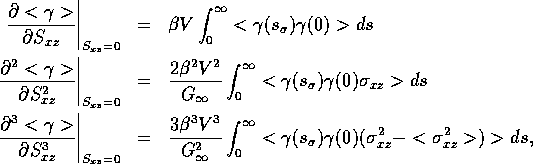 is
antisymmetric, and J is symmetric. Thus the Burnett coefficients
simplify to
is
antisymmetric, and J is symmetric. Thus the Burnett coefficients
simplify to

where  and
and
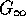
with 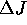 being the infinite frequency shear modulus [Brown and
Clarke
[1986]]
.
being the infinite frequency shear modulus [Brown and
Clarke
[1986]]
.