In order to establish the feasibility of calculations based on equations
(
), it was decided to perform a calculation using the colour
conductivity model described in section . The intermolecular
potential was taken to be the Lennard-Jones potential, which has an attractive
component due to van der Waals interaction, and a repulsive hard core that
goes as 
:
In what follows, every quantity will be given in reduced units, in which
.
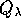The system consists of 108 particles at a temperature of 1.08 and density of 0.85. This state point was chosen because considerable information was already known about this system at that state point [Evans and Morriss
[1985], and references therein] .
The equations of motion employed were the Nosé-Hoover feedback mechanism for
the Norton ensemble (eq ). The feedback parameter
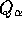was chosen to be of order unity, and 
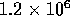to be 3.24.
The values of
these parameters were chosen to give optimal convergence of the linear
response function. There is no real reason for them to be optimal for
non-linear response functions.
The code used is reported in appendix . When finally optimized,
it executed 
timesteps per hour, or about 75 Mflops on the
Fujitsu VP100 computer. Even so, hundreds of hours of CPU time were required
to establish reasonable statistics for the response functions. Clearly,
computers of one to two orders of magnitude greater power are required for
these calculations to be practical. Already, the next generation of
supercomputers promise this power.
Figure shows 
for the system under study for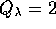 
and 
.
One immediately notices that the
non-linear response lasts much longer than the linear case, with the integral
converging by a time of 8, compared with unity in the case of the linear
response, which is shown in figure for the same system.
The
agreement of these results for different values of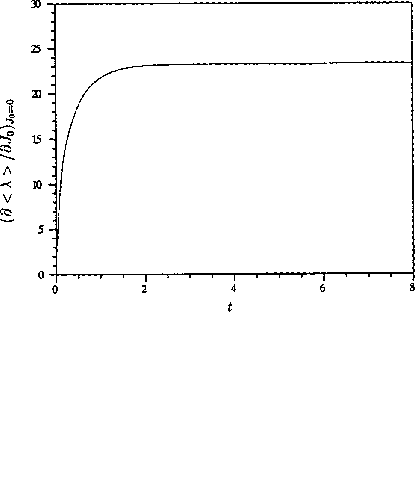 
within statistical uncertainty indicates that a
true value has been found for the third order coefficient.
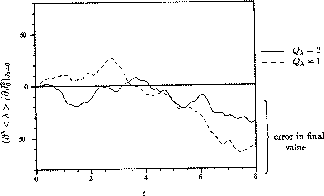
Figure:
Linear response for colour conductivity
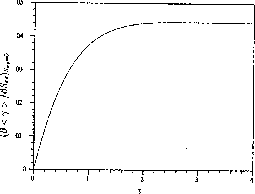
Figure:
Third order nonlinear response for colour conductivity
Figure:
Linear response for planar Couette flow
Figure:
Third order nonlinear response for planar couette flow
Evans (private communication) has run a similar simulation on a planar Couette
flow system, using code that is described in Hood [1989]. Figure
shows the third order response 
for 
, 150 and 200.
The linear response for the system is shown in figure
The good agreement between these results indicates that the
calculation is feasible. Unfortunately, we don't have sufficient evidence to
tackle the question of divergences in the Burnett coefficients. It has been
suggested [van Beijeren, private communication] that the coefficients may
diverge in the thermodynamic limit. To test this hypothesis requires rerunning
the code at different system sizes, something that is impractical at current
processor speeds.