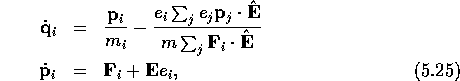Next: Colour Current
Up: Models of Nonequilibrium
Previous: Models of Nonequilibrium
Planar Couette flow occurs when the steady state streaming velocity,  ,
is a linear function of position
,
is a linear function of position 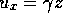 . In particular, assume
. In particular, assume
 . Shear flow, like all Navier-Stokes transport processes, is
driven by boundary conditions (e.g. moving walls). This is inconvenient for
computer simulations because of the huge surface effects that would be induced
in the small systems which we are capable of simulating on computers (
. Shear flow, like all Navier-Stokes transport processes, is
driven by boundary conditions (e.g. moving walls). This is inconvenient for
computer simulations because of the huge surface effects that would be induced
in the small systems which we are capable of simulating on computers ( ).
).
Computer simulation of equilibrium systems has always employed periodic
boundary conditions to minimize size dependence effects. Figure
 illustrates a way of adapting periodic boundary conditions
to planar Couette flow. The so-called Lees-Edwards periodic boundary
conditions [Lees and Edwards
[1972]]
employ time
varying nonorthogonal lattice vectors. The perpendicular height of the cells
remains fixed so that the shearing deformation occurs isochorically. Once
illustrates a way of adapting periodic boundary conditions
to planar Couette flow. The so-called Lees-Edwards periodic boundary
conditions [Lees and Edwards
[1972]]
employ time
varying nonorthogonal lattice vectors. The perpendicular height of the cells
remains fixed so that the shearing deformation occurs isochorically. Once
 , it may be reset to 0
, it may be reset to 0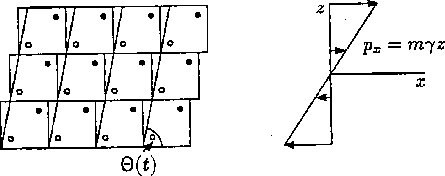 without changing the
mutual disposition of particles. If a particle exits a cell through a top
face, it is replaced by its periodic image which enters at the bottom face.
This image will be positioned according to the current angle of the slewing
lattice vector. The x-component of its velocity will be the old velocity
minus the strain rate multiplied by the perpendicular height of the cell. Its
peculiar velocity ( i.e. relative to the planar velocity profile) is
unchanged.
without changing the
mutual disposition of particles. If a particle exits a cell through a top
face, it is replaced by its periodic image which enters at the bottom face.
This image will be positioned according to the current angle of the slewing
lattice vector. The x-component of its velocity will be the old velocity
minus the strain rate multiplied by the perpendicular height of the cell. Its
peculiar velocity ( i.e. relative to the planar velocity profile) is
unchanged.

Figure:
Lees-Edwards Periodic Boundary Conditions for Planar Couette Flow
This is all that is really needed to run a molecular dynamics simulation of
planar Couette flow at low Reynolds number. Reynolds number The
flow of the periodic particles above and below the primitive cell will try to
induce a linear velocity profile in the system. One simply solves Newton's
equations of motion for the system of N interacting particles, waits for the
initial transients to decay, and then accumulates statistical averages for the
shear stress, the energy, etc.
Of course such a system will heat up. It will never achieve a steady state. To
remedy this, we may employ a Gaussian or Nosé-Hoover thermostat. We must be
careful, however, to ensure that it is the peculiar velocities which are
thermostatted, and not the laboratory velocities. If the Reynolds number
is sufficiently small so that a linear velocity profile is stable, the
streaming velocity will be 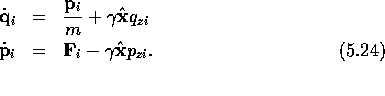 .
.
The so-called SLLOD equations provide a more convenient and more elegant set
of variables with which to work. The first advantage of the SLLOD equations of
motion is that they only involve the coordinates and the peculiar
momenta of the particles. Since the thermostat, the internal energy and the
pressure all involve peculiar, rather than laboratory velocities, this is an
advantage.
The second advantage is that SLLOD momenta are continuous as particles leave
and enter the primitive cell, as the calculation is more stable than it
otherwise might be.
The SLLOD equations of motion are:

Differentiating the 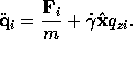 equation gives:
equation gives:
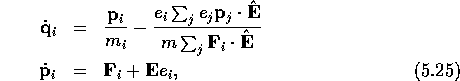
Thus, except at t=0, when the shear rate is switched on, the SLLOD equations
of motion are simply Newton's. Once the shear motion has impulsively started
at t=0, the Lees-Edwards boundary conditions continue the shear flow motion.
The third
advantage of the SLLOD equations is that they transform a boundary driven
system to one with an external field, which makes the system more amenable to
theoretical analysis.





Next: Colour Current
Up: Models of Nonequilibrium
Previous: Models of Nonequilibrium
Russell Standish
Thu May 18 11:43:52 EST 1995
 ,
is a linear function of position
,
is a linear function of position 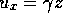 . In particular, assume
. In particular, assume
 . Shear flow, like all Navier-Stokes transport processes, is
driven by boundary conditions (e.g. moving walls). This is inconvenient for
computer simulations because of the huge surface effects that would be induced
in the small systems which we are capable of simulating on computers (
. Shear flow, like all Navier-Stokes transport processes, is
driven by boundary conditions (e.g. moving walls). This is inconvenient for
computer simulations because of the huge surface effects that would be induced
in the small systems which we are capable of simulating on computers ( ).
).
 , it may be reset to 0
, it may be reset to 0 without changing the
mutual disposition of particles. If a particle exits a cell through a top
face, it is replaced by its periodic image which enters at the bottom face.
This image will be positioned according to the current angle of the slewing
lattice vector. The x-component of its velocity will be the old velocity
minus the strain rate multiplied by the perpendicular height of the cell. Its
peculiar velocity ( i.e. relative to the planar velocity profile) is
unchanged.
without changing the
mutual disposition of particles. If a particle exits a cell through a top
face, it is replaced by its periodic image which enters at the bottom face.
This image will be positioned according to the current angle of the slewing
lattice vector. The x-component of its velocity will be the old velocity
minus the strain rate multiplied by the perpendicular height of the cell. Its
peculiar velocity ( i.e. relative to the planar velocity profile) is
unchanged.

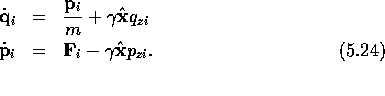 .
.

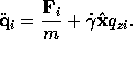 equation gives:
equation gives: