




Next: Formal Solution of
Up: Nonequilibrium Molecular Dynamics
Previous: Nonequilibrium Molecular Dynamics
Consider a classical system of N particles. The state of the
system is uniquely specified by the 3N spatial co-ordinates
 ,
,  ,
, 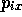 and the 3N momentum co-ordinates
and the 3N momentum co-ordinates
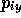 ,
, 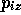 ,
, 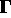 . The 6N dimensional vector
. The 6N dimensional vector 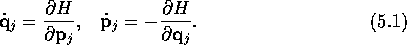 consisting of the positions and momenta for all
particles is a point in the phase space of the system. The
dynamics of the system evolving in time is described by the
trajectory of the phase point through phase space. The trajectory
is given by Hamilton's equations:
consisting of the positions and momenta for all
particles is a point in the phase space of the system. The
dynamics of the system evolving in time is described by the
trajectory of the phase point through phase space. The trajectory
is given by Hamilton's equations:

Linear transport coefficients, (e.g.  and
and 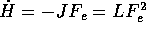 )
can be calculated from computer simulations of molecules obeying eq.
(
)
can be calculated from computer simulations of molecules obeying eq.
( ) by means of
the Green-Kubo relations. These have proved to be of enormous value in
experimental and theoretical applications. If we wish to extend the theory to
non-linear steady states, then we are faced with two problems; one being the
inclusion of higher order terms in the perturbation due to the external field,
and the other due to thermostatting. In a dissipative process, such as shear
flow, the temperature would rise in the system if the heat generated is not
removed by a heat sink. This effect is second order in the small field limit
(
) by means of
the Green-Kubo relations. These have proved to be of enormous value in
experimental and theoretical applications. If we wish to extend the theory to
non-linear steady states, then we are faced with two problems; one being the
inclusion of higher order terms in the perturbation due to the external field,
and the other due to thermostatting. In a dissipative process, such as shear
flow, the temperature would rise in the system if the heat generated is not
removed by a heat sink. This effect is second order in the small field limit
( , with L being the linear transport coefficient relating
, with L being the linear transport coefficient relating  to J), and can be ignored in the linear theory, but needs to be included in
non-linear theories.
to J), and can be ignored in the linear theory, but needs to be included in
non-linear theories.
The most obvious way of modelling the non-equilibrium steady state is to
include the interactions of the system with the outside world. This method is
impractical owing to the high complexity of these interactions, and the large
surface effects inherent in modelling small systems (computer simulations
typically involve  to
to  molecules). It turns out that the heat
sink can be modelled by means of a friction-like term, which acts as a
thermostat, and that provided the dissipation is not too large, the Transient
Time Correlation Functions we will derive are independent of what model
thermostat is used [Evans and Morriss
[1984], Evans
and Holian
[1985]]
.
molecules). It turns out that the heat
sink can be modelled by means of a friction-like term, which acts as a
thermostat, and that provided the dissipation is not too large, the Transient
Time Correlation Functions we will derive are independent of what model
thermostat is used [Evans and Morriss
[1984], Evans
and Holian
[1985]]
.
The thermostatted equations of motion are

where  describes the force on molecule i due to all the other
molecules. The momenta in this equation are peculiar ,
i.e. measured with respect to the motion of the centre of mass so that
describes the force on molecule i due to all the other
molecules. The momenta in this equation are peculiar ,
i.e. measured with respect to the motion of the centre of mass so that
 .
The first model thermostat is produced by requiring that the kinetic energy be
a constant of motion:
.
The first model thermostat is produced by requiring that the kinetic energy be
a constant of motion:
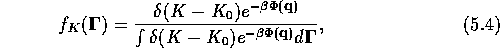
This is known as the Gaussian thermostat, after Gauss's principle of least
constraint [Hoover et al.
[1982]
, Evans
[1983]]
.
This feedback mechanism does not constrain the actual value of the
kinetic energy required, it only constrains the time derivative to be zero.
This implies that the propagator (to be defined in the next section) will
commute with the operation of differentiation with respect to temperature,
allowing equilibrium fluctuation expressions for the second order, or derived
thermodynamic quantities, such as specific heats. Such a thermostat is called
differential.
The equilibrium distribution in this case is given by

where 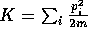 ,
,  ,
, 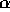 .
This distribution is called the isokinetic distribution.
.
This distribution is called the isokinetic distribution.
The other common thermostatting method was first proposed by Nosé
[1984a,1984b]. The original formulation by Nosé involved a cumbersome
external reservoir and a non-linear time transformation. Hoover
[1985] made significant simplifications to the method, which has
since become known as the Nosé-Hoover thermostat. The basic idea is to
extend phase space by adding the variable  , whose equation of motion
is given by
, whose equation of motion
is given by

Thus 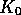 acts to keep the kinetic energy fluctuating about the
target value
acts to keep the kinetic energy fluctuating about the
target value  , with the timescale of the fluctuations being proportional
to Q. The parameter Q is arbitrary, but the Q=0 case, which corresponds
to the kinetic energy being rigidly constrained, has infinitely stiff
equations of motion. In practice, its value is determined from numerical
experiments. The equilibrium distribution generated by the Nosé-Hoover
equations of motion is canonical:
, with the timescale of the fluctuations being proportional
to Q. The parameter Q is arbitrary, but the Q=0 case, which corresponds
to the kinetic energy being rigidly constrained, has infinitely stiff
equations of motion. In practice, its value is determined from numerical
experiments. The equilibrium distribution generated by the Nosé-Hoover
equations of motion is canonical:

where  .
In contrast to the former thermostat, this is an integral thermostat, with the
value of
.
In contrast to the former thermostat, this is an integral thermostat, with the
value of  depending on all past states of the system.
depending on all past states of the system.





Next: Formal Solution of
Up: Nonequilibrium Molecular Dynamics
Previous: Nonequilibrium Molecular Dynamics
Russell Standish
Thu May 18 11:43:52 EST 1995
 ,
,  ,
, 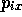 and the 3N momentum co-ordinates
and the 3N momentum co-ordinates
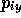 ,
, 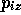 ,
, 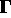 . The 6N dimensional vector
. The 6N dimensional vector 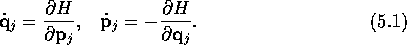 consisting of the positions and momenta for all
particles is a point in the phase space of the system. The
dynamics of the system evolving in time is described by the
trajectory of the phase point through phase space. The trajectory
is given by Hamilton's equations:
consisting of the positions and momenta for all
particles is a point in the phase space of the system. The
dynamics of the system evolving in time is described by the
trajectory of the phase point through phase space. The trajectory
is given by Hamilton's equations:

 and
and 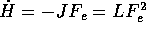 )
can be calculated from computer simulations of molecules obeying eq.
(
)
can be calculated from computer simulations of molecules obeying eq.
( , with L being the linear transport coefficient relating
, with L being the linear transport coefficient relating  to J), and can be ignored in the linear theory, but needs to be included in
non-linear theories.
to J), and can be ignored in the linear theory, but needs to be included in
non-linear theories.
 to
to  molecules). It turns out that the heat
sink can be modelled by means of a friction-like term, which acts as a
thermostat, and that provided the dissipation is not too large, the Transient
Time Correlation Functions we will derive are independent of what model
molecules). It turns out that the heat
sink can be modelled by means of a friction-like term, which acts as a
thermostat, and that provided the dissipation is not too large, the Transient
Time Correlation Functions we will derive are independent of what model

 describes the force on molecule i due to all the other
molecules. The momenta in this equation are peculiar
describes the force on molecule i due to all the other
molecules. The momenta in this equation are peculiar .
The first model thermostat is produced by requiring that the kinetic energy be
a constant of motion:
.
The first model thermostat is produced by requiring that the kinetic energy be
a constant of motion:
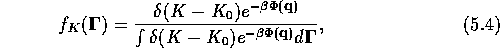

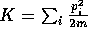 ,
,  ,
, 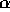 .
This distribution is called the isokinetic distribution.
.
This distribution is called the isokinetic distribution.
 , whose equation of motion
is given by
, whose equation of motion
is given by

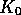 acts to keep the kinetic energy fluctuating about the
target value
acts to keep the kinetic energy fluctuating about the
target value  , with the timescale of the fluctuations being proportional
to Q. The parameter Q is arbitrary, but the Q=0 case, which corresponds
to the kinetic energy being rigidly constrained, has infinitely stiff
equations of motion. In practice, its value is determined from numerical
experiments. The equilibrium distribution generated by the Nosé-Hoover
equations of motion is canonical:
, with the timescale of the fluctuations being proportional
to Q. The parameter Q is arbitrary, but the Q=0 case, which corresponds
to the kinetic energy being rigidly constrained, has infinitely stiff
equations of motion. In practice, its value is determined from numerical
experiments. The equilibrium distribution generated by the Nosé-Hoover
equations of motion is canonical:

 .
In contrast to the former thermostat, this is an integral thermostat, with the
value of
.
In contrast to the former thermostat, this is an integral thermostat, with the
value of  depending on all past states of the system.
depending on all past states of the system.