The general principle of this experiment is that a narrow pulse of charged particles is injected into the drift region, and the resulting distribution of charged particles is observed at some time later. By taking the final observation at different times, a picture can be built up of how a pulse evolves in time. The drift velocity is usually calculated by finding the time that the swarm's peak takes to traverse a certain distance.
Many methods have been used to measure drift velocities, but
this thesis will only be concerned with the
electrical shutter method. The shutters usually consist either of a pair of
wire gauzes, as in the Tyndell-Powell method, or of a grid of wires of
alternating polarity as in the more accurate Bradbury-Nielson method (see fig.
).
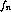
Figure:
Bradbury-Nielsen shutter
The first shutter opens to let the swarm into the drift region. The
particles then drift and diffuse in a uniform electric field to a
second shutter which samples the charged particle flux at some time
after the pulse was transmitted through the first shutter (see
fig. ). The distance between the shutters may be varied to
measure the swarm density as a function of distance, as well as time.
The shutters are usually operated by applying either a sine or
square wave of variable frequency. The arrival time spectrum is
obtained by measuring the current as a function of the shutter
frequency. This consists of a series of peaks at frequencies,
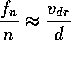, which in the case of the Tyndell-Powell method satisfy the relation
where n is an integer, 
the drift velocity, and d
the distance between the shutters.
In the Bradbury-Nielson technique, the frequencies are effectively doubled, as
the shutter is open when the shutter control signal passes through zero, and
closed when a voltage of either polarity is applied to the shutter.
Figure:
Time of flight experiment with shutters. A typical arrival time spectrum is
shown