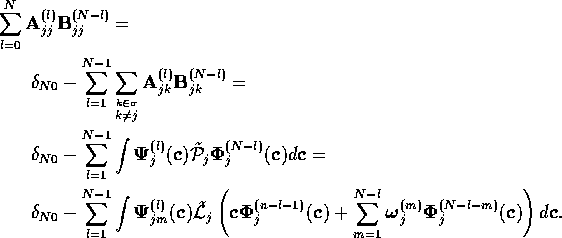Next: Isotropic Tensors
Up: Perturbation of the
Previous: Consistency with Biorthonormality
From ( ), one can see that
), one can see that 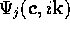 and hence
and hence 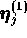 is
dependent on the choice of an arbitrary term
is
dependent on the choice of an arbitrary term 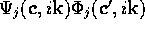 . However, the product
. However, the product 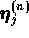 is invariant under choice of
any of the arbitrary terms
is invariant under choice of
any of the arbitrary terms 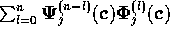 ,
which we will now demonstrate by induction for the
non-degenerate case. The extension to the degenerate case is straightforward.
,
which we will now demonstrate by induction for the
non-degenerate case. The extension to the degenerate case is straightforward.
We need to prove that the Taylor series coefficients of the
product are invariant, i.e. that 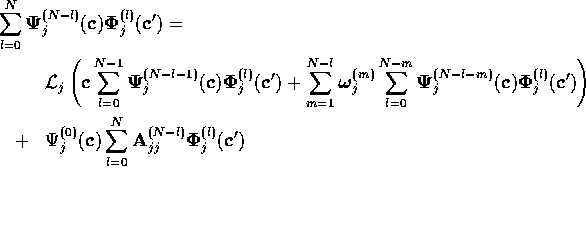 is invariant
for every n. This is clearly true for n=0. Assume that
this is true for all n less than some whole number N. Then we find
is invariant
for every n. This is clearly true for n=0. Assume that
this is true for all n less than some whole number N. Then we find

by use of ( ). The first term on the right
hand side is invariant by hypothesis. Now consider the second
term, and suppose that
). The first term on the right
hand side is invariant by hypothesis. Now consider the second
term, and suppose that 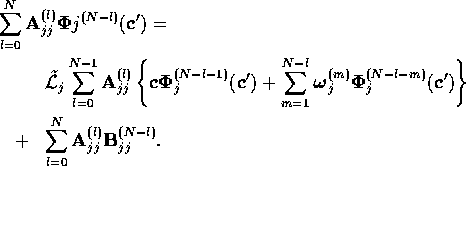 is invariant for all n less than N,
as it is clearly true for n=0. Then
is invariant for all n less than N,
as it is clearly true for n=0. Then
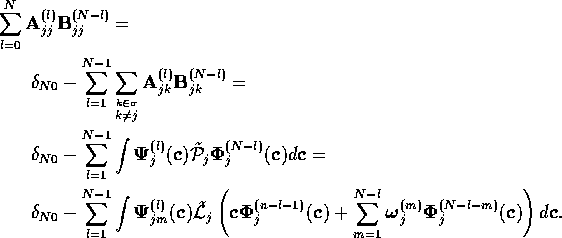
The first term of the right hand side is invariant by
hypothesis, so we only need consider the second term

Clearly, this term is invariant by hypothesis, so

is invariant.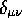
Russell Standish
Thu May 18 11:43:52 EST 1995
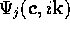 and hence
and hence 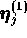 is
dependent on the choice of an arbitrary term
is
dependent on the choice of an arbitrary term 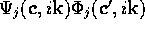 . However, the product
. However, the product 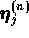 is invariant under choice of
any of the arbitrary terms
is invariant under choice of
any of the arbitrary terms 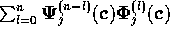 ,
which we will now demonstrate by induction for the
non-degenerate case. The extension to the degenerate case is straightforward.
,
which we will now demonstrate by induction for the
non-degenerate case. The extension to the degenerate case is straightforward.
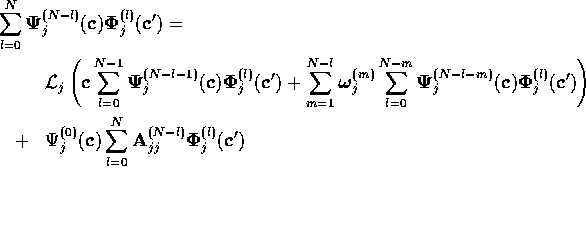 is invariant
for every n. This is clearly true for n=0. Assume that
this is true for all n less than some whole number N. Then we find
is invariant
for every n. This is clearly true for n=0. Assume that
this is true for all n less than some whole number N. Then we find

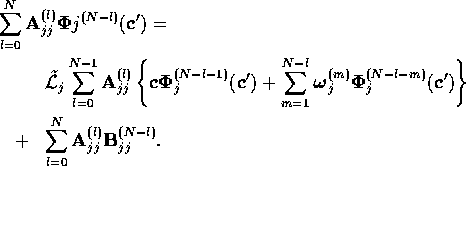 is invariant for all n less than N,
as it is clearly true for n=0. Then
is invariant for all n less than N,
as it is clearly true for n=0. Then