




Next: Formal Solution of
Up: The Linear Boltzmann
Previous: Time Dependent Transport
Since we are interested in obtaining 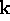 for
small values of
for
small values of 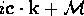 , it is reasonable to assume that
, it is reasonable to assume that  also admits a complete set of
eigenfunctions, at least for sufficiently small
also admits a complete set of
eigenfunctions, at least for sufficiently small  . The
adjoint operator
. The
adjoint operator  will
then admit a complete set of eigenfunctions that are biorthogonal
with those of
will
then admit a complete set of eigenfunctions that are biorthogonal
with those of 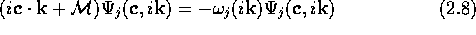 :
:
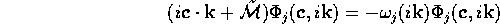


These eigenfunctions may be used as a basis set for finding the solution
function 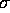 , as in equation
(
, as in equation
( ).
).
The index j takes values from a set 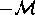 , which is isomorphic to
the natural numbers, as the spectrum is assumed discrete.
Let the index 0 denote the eigenvalue of
, which is isomorphic to
the natural numbers, as the spectrum is assumed discrete.
Let the index 0 denote the eigenvalue of 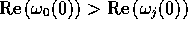 with largest real
value,
i.e.
with largest real
value,
i.e. 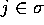 for every
other
for every
other 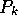 . Then, we define a projection operator
. Then, we define a projection operator  , which
projects out the hydrodynamic (long time) part of the Fourier
transform of a phase space distribution
, which
projects out the hydrodynamic (long time) part of the Fourier
transform of a phase space distribution  by
by
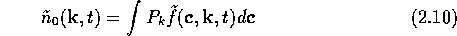
The k-space density function can now be split into a hydrodynamic part
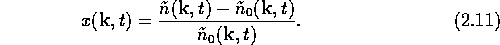
and a non-hydrodynamic part

The Taylor series coefficients of 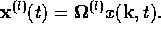 are denoted by
are denoted by

These can be computed from the Taylor coefficients  ,
,
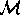 , which can be computed from the eigenfunctions of
, which can be computed from the eigenfunctions of
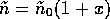 by means of a recursion method (see Appendix
by means of a recursion method (see Appendix  ).
Substituting
).
Substituting 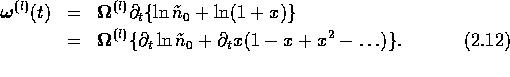 into (
into ( ), the time dependent transport coefficients become
), the time dependent transport coefficients become

Russell Standish
Thu May 18 11:43:52 EST 1995
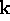 for
small values of
for
small values of 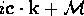 , it is reasonable to assume that
, it is reasonable to assume that  also admits a complete set of
eigenfunctions, at least for sufficiently small
also admits a complete set of
eigenfunctions, at least for sufficiently small  . The
adjoint operator
. The
adjoint operator  will
then admit a complete set of eigenfunctions that are biorthogonal
with those of
will
then admit a complete set of eigenfunctions that are biorthogonal
with those of 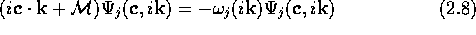 :
:
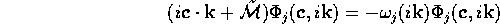


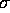 , as in equation
(
, as in equation
(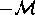 , which is isomorphic to
the natural numbers, as the spectrum is assumed discrete.
Let the index 0 denote the eigenvalue of
, which is isomorphic to
the natural numbers, as the spectrum is assumed discrete.
Let the index 0 denote the eigenvalue of 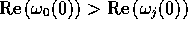 with largest real
value,
i.e.
with largest real
value,
i.e. 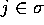 for every
other
for every
other 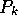 . Then, we define a projection operator
. Then, we define a projection operator  , which
projects out the hydrodynamic (long time) part of the Fourier
transform of a phase space distribution
, which
projects out the hydrodynamic (long time) part of the Fourier
transform of a phase space distribution  by
by
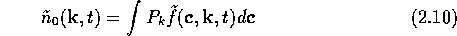
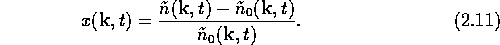

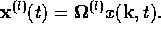 are denoted by
are denoted by

 ,
,
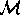 , which can be computed from the eigenfunctions of
, which can be computed from the eigenfunctions of
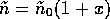 by means of a recursion method (see Appendix
by means of a recursion method (see Appendix 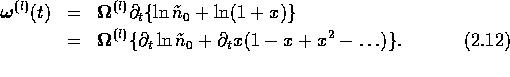 into (
into (